統計処理を行う際に、ノンパラかパラメトリックかどうかを把握する必要がありました
これを正規分布している・していない、と表現しますが、正規分布していない場合には、データが両端にバラついている度合いが大きくなるということになります
正規分布の場合でも、多少はデータは散らばります
このようにデータがばらついていることを散布度と呼びます
今回はデータのばらつきを表す散布度について解説しつつ、pythonでどのように表現するのかをサンプルコードを交えつつ紹介していきたいと思います
pythonで統計学を順序立てて学びたい方は、こちらの記事を参考に進めてみてください
データのばらつきを表す散布度とは
散布度はデータがどれくらい散らばっているかを表しています
以前解説したデータの代表値だけでは、散布度はわからないため、改めて散布度をみる必要が出てきます
そのため、代表値とともに散布度も一緒に算出する必要があります
散布度として用いる指標には、以下のようなものがあります
- 四分位範囲
- 四分位偏差
- 範囲
- 分散
- 標準偏差
今回の記事では、四分位範囲・四分位偏差・範囲について解説をしたいと思います
データの範囲
データの範囲(range)とは、最大値-最小値のことを指します
irisのデータを使って説明していきますので、まずはirisのデータを用意して、最大値と最小値を求めます
import pandas as pd
iris = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv')
#irisの先頭5行を確認
print(iris.head())
#.max()で最大値,.min()で最小値を求める
print(iris.max())
print(iris.min())
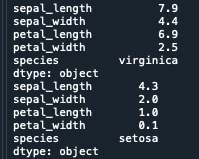
今回はsepal_lengthの範囲を求めたいと思います
求めるデータが少なかったり、桁が小さければ自力で計算するのでもありですが、そういった計算もpythonに任せてしまいましょう
import pandas as pd
iris = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv')
datarange=iris["sepal_length"].max()-iris["sepal_length"].min()
print("sepal_lengthの範囲は",datarange)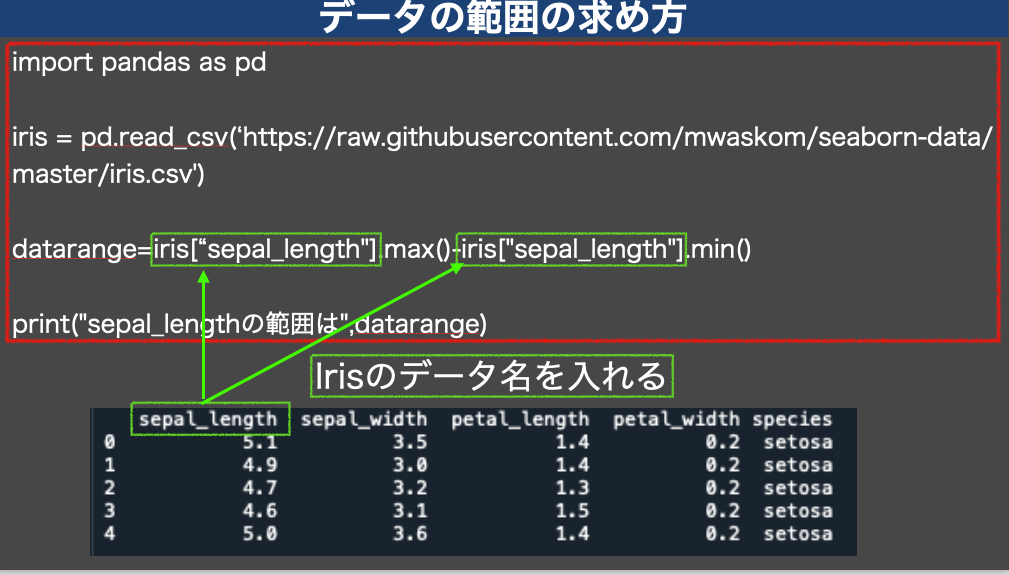
iris.[“XXXX”]のXXXX部分を変えれば、他のデータでも同じように算出することができます
irisの部分は読み込んだ変数名になっています
四分位範囲と四分位偏差
最大値と最小値から求める範囲の弱点は、外れ値に左右されてしまう、という点です
そこで出てくるのが、四分位数を使った四分位範囲と四分位偏差です
四分位数はデータを順番に並べたときに4等分するというものです
このとき4等分にした数値である四分位数を使って、四分位範囲(interquartile range: IQR)を求めます
また、四分位範囲の半分の値を四分位偏差(quartile deviation: QD)と呼びます
さらに、第二四分位数は中央値になります
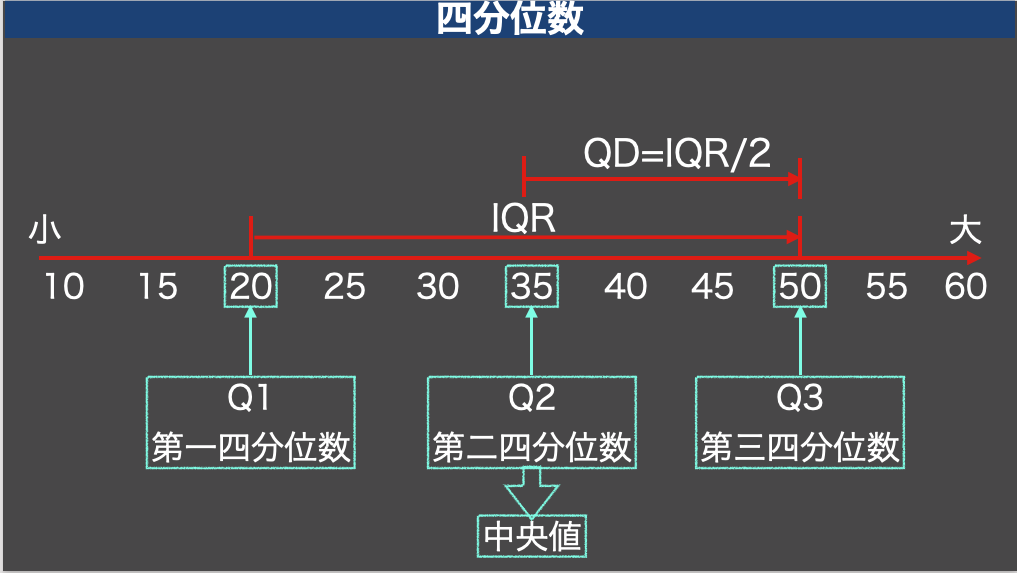
四分位範囲や四分位偏差もデータのばらつきを確認する指標であり、外れ値の影響をあまり受けないというメリットがあります
pythonではscipy.stats.iqr()を使えば簡単に算出することができます
from scipy import stats
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns; sns.set()
iris = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv')
iqr=stats.iqr(iris["sepal_length"])
qd=iqr/2
#箱ひげ図の作成
sns.boxplot(iris["sepal_length"])
plt.show()
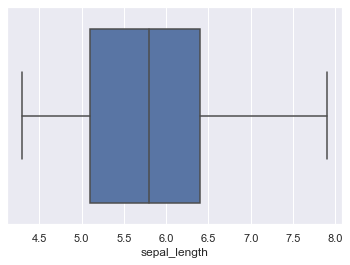
基本的にノンパラのデータであれば、四分位数を使い、箱ひげ図で可視化すると私は学びました
平均値と棒グラフでは、両端の数値に左右されやすいからです
ぜひpythonでデータのばらつきを表現してみてください
まとめ
- データの範囲:最大値-最小値(外れ値に左右される)
- 四分位数:データを並べたときの4等分にした値
- 第二四分位数は中央値
- 四分位範囲(IQR):第三四分位数-第一四分位数
- 四分位偏差:IQRの半分













