統計検定を行うと出てくるのが「t値」と「p値」です
多くの場合「p値」について理解していれば、研究結果を述べることができるかと思います
私もそうですし、学会や論文なんかでも「p値」のみに言及していることが多いです
しかし、統計の勉強を進めていくと「t値」を理解しなければいけないタイミングがやってきます
今回は「p値」のおさらいと「t値」について解説をしていきたいと思います
これまでの「pythonで統計学」の一覧はこちらから見ることができるので、そちらも参考にしてください!
t値は検定統計量の1種で、仮説検定において標本データから計算される標準化された値
t値の理解にはt分布の理解が必要
p値は帰無仮説を棄却する目安
t値とは
t値は検定統計量の1種で、t検定を行った際に出てきます
そのため「t値」と呼ばれています
マンホイットニーのU検定などをかけても「t値」は出てきません
以下を見比べるとわかります


t値の算出は、
t値=標本平均-比較対象値/標準誤差
で求めることができます
t値が0である場合には標本の結果が帰無仮説と完全に一致することを示していることになります
標本データと帰無仮説との差が増加すれば、t値の絶対値は増加していきます
t値単体ではあまり判断材料にはしません
ここでt分布という理解が必要になってきます
t分布とは
t分布とは「平均𝑥¯の標本分布において,母集団の標準偏差𝜎の代わりに標本標準偏差𝑠′を用いた場合の標準化後の平均𝑥¯が従う確率分布」です
ざっくりいうと、標準正規分布の代わりになるのが、t分布ということになります
>>>標準正規分布について(…coming soon…)
言葉だけではわかりにくいので、実際にt分布をpythonで書いてみたいと思います
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# -10 から 10 の区間で200列の一次元配列を作成
x = np.linspace(-10, 10, 200)
# サブプロットを用意
fig, ax = plt.subplots(1, 1)
# 自由度(1, 3, 30)の3つのt分布をプロット
deg_of_freedom = [1, 3, 30]
for k in deg_of_freedom:
ax.plot(x, stats.t.pdf(x, k), label=r'$k=%i$' % k)
plt.xlim(-10, 10)
plt.ylim(0, 0.4)
plt.legend()
plt.show()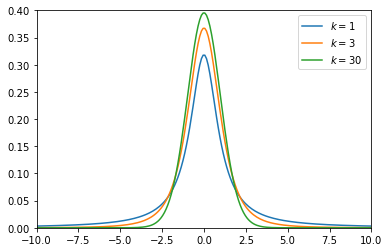
kが自由度を表していますが、自由度の値が大きくなるにつれてt分布がシャープになっているのがわかるかと思います
t分布はサンプルサイズが少ない(n=30以下)場合に用いる、と言われています
サンプルサイズが増えるにつれて、予測される平均値のブレが少なくなるため、シャープになっていきます
次に標準正規分布とt分布を比較してみたいと思います
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
x = np.linspace(-10, 10, 100)
z = stats.norm.pdf(x, loc=0, scale=1)
for k in range(1, 10, 4):
t = stats.t.pdf(x, k)
plt.plot(x, t, label=f'$k=%i$' % k)
plt.plot(x, z, label='std norm', linewidth=3)
plt.legend()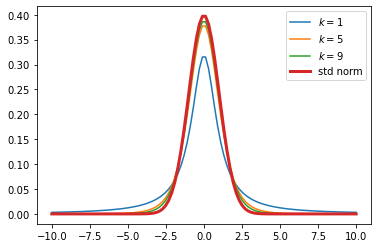
太い赤い線が標準正規分布なので、自由度が増加すると、t分布は標準正規分布に近似していくことがわかります
こういった背景があるため、サンプルサイズが増えた場合には、t分布ではなく、標準正規分布を使用してもOKだよね、となります
t分布から区間推定を行う
ではt分布から信頼区間を算出したいと思います
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
x = np.linspace(-5, 5, 100)
left, right = stats.t.interval(0.95, df=2)
t = stats.t.pdf(x, df=2)
plt.plot(x, t)
plt.axvline(left, c='r')
plt.axvline(right, c='r')
print(left, right)
>>>-4.302652729911275 4.302652729911275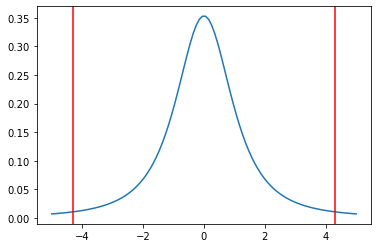
信頼区間の幅が結構大きいのがわかるかと思います
自由度が小さい(今回は自由度2)場合には、区間も広くなってしまいます
では、自由度を大きくしてみたいと思います
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
x = np.linspace(-5, 5, 100)
left, right = stats.t.interval(0.95, df=100)
t = stats.t.pdf(x, df=100)
plt.plot(x, t)
plt.axvline(left, c='r')
plt.axvline(right, c='r')
print(left, right)
>>>-1.9839715184496334 1.9839715184496334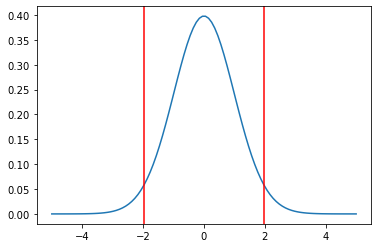
1枚目と2枚目の赤線の間が95%区間です
自由度が大きくなるにつれて、95%区間が狭くなるのがわかるかと思います
基本的にはt分布を使用することが推奨されています
しかし、自由度が高くなる(サンプルサイズが増える)と標準正規分布に近づくため、標準正規分布が使用されます
統計ソフトのほとんどが「正規性の検定」で正規分布をしているかを確認しているので、そちらを使うのがいいと思います
pythonなどのプログラミング言語で統計をかける場合には、t分布を用いるのがいいのかな、と思います
p値について
p値は多くの人が聞いたことのある単語だと思います
帰無仮説を棄却する値ですね

95%の確率でその事象が生じると仮定した場合に、
5%未満であった場合には「滅多に起こらないことが起きた(つまり帰無仮説が間違っていたのではないか)」ということで対立仮説を採択することになります
帰無仮説・対立仮説などのややこしい考え方は、背理法が元になっているので、
興味がある方は、背理法について学んでみてください
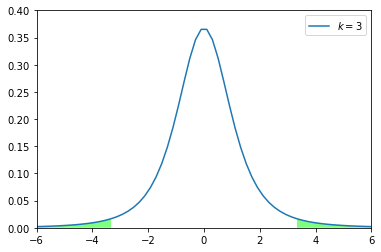
95%というのは、緑で塗りつぶしていない部分が該当します
基本的にはこの範囲に事象が入りうるというのが基本になっています
まとめ
- t分布は,平均𝑥¯の標本分布において,母集団の標準偏差𝜎の代わりに標本標準偏差𝑠′を用いた場合の標準化後の平均𝑥¯が従う確率分布
- t分布は自由度n-1を唯一のパラメータとする確率分布
- 自由度を大きくすると徐々に標準正規分布に近づく









