統計的仮説検定を行う場合には、あらかじめサンプルサイズを決めておく必要があります
サンプルサイズとは研究対象者のことで、
少なすぎると有意差があるのに、有意差が出なかったり、
多すぎると有意差がないのに、有意差が出たりします
そのため、あらかじめサンプルサイズを決めておくことは、とても重要になります
今回の記事では、pythonを使ってサンプルサイズを求める方法を解説していきたいと思います
サンプルコードもあるので、実際に手を動かしながら試してみてください!
サンプルサイズとは
サンプルサイズとは、研究対象者のことを指します
よくn=xxxと表記されているものです
サンプルサイズは大きくなるにつれて標本誤差が減少していくという特徴を持っています
間違えやすいのがサンプル数です
サンプル数は標本の数なので、間違えないようにしておきましょう
また、研究対象者を集まるだけ集める、というのは倫理的に好ましくないです
研究対象者の時間を奪っているので、必要な人数だけデータを取るのが推奨されます
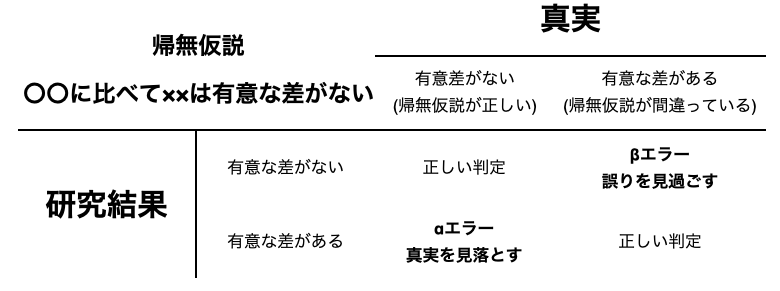
サンプルサイズを誤るとエラーが出る
サンプルサイズを求めなくてはいけないのは、サンプルサイズを誤るとエラーが出るためです
このエラーをαエラー(第1種の過誤)、βエラー(第2種のエラー)と呼びます
αエラーはサンプルサイズが少ない場合におきます
本来は有意差があるはずなのに、有意差がないという結果が出てしまう場合です
βエラーはサンプルサイズが大きすぎる場合におきます
本来は有意差がないはずなのに、有意差があるという結果が出てしまいます
pythonでサンプルサイズを求める
では実際にサンプルサイズを求めたいと思います
検定の種類によっていくつかに分かれています
import statsmodels.stats.power as smp
#平均値に関するt検定(1,2標本,対応あり)
# 平均値の差
delta = 0.5
# 標準偏差
sd = 1
# 有意水準
sig = 0.05
# 検定力
power = 0.8
# 効果量 (平均値の差 / 標準偏差 )
effect_size = delta / sd
# 両側検定
alternative='two-sided'
n = smp.tt_ind_solve_power(effect_size=effect_size, alpha=sig, power=power, alternative=alternative)
print(n)
#サンプルサイズの異なる2群の平均値に関するt検定
# 有意水準
sig = 0.05
# 検定力
power = 0.8
# 効果量
effect_size = 0.6
# レシオ サンプルサイズは、2:3
ratio = 60./90
# 両側検定
alternative='two-sided'
n = smp.tt_ind_solve_power(effect_size=effect_size, alpha=sig, power=power, alternative=alternative, ratio=ratio)
print("alternative=two-sided: ", n)
有意水準、検定力は任意の数値で大丈夫です
基本的には有意水準0.05が一般的です
また、検定力は0.8が推奨されています
参考文献はこちらから
It is proposed here as a convention that, when the investigator has no other basis for setting the desired power value, the value .80 be used.
(ここでは,分析者が望む検出力を設定するための他の根拠がない場合,値.80を使用することを慣習として提案する。)p56より
便利なのがG power
pythonでサンプルサイズを求めることもできますが、もっと便利なのが「G power」です
G powerはサンプルサイズを求めるのに特化した無料ソフト
これは使い方の資料もネット上に置いてあるので、それをみるだけで、操作ができます
pythonで一度サンプルサイズを求められるようになったら、G powerを使うのがいいかもです
まとめ
- pythonでサンプルサイズを求めるときは、statsmodels.stats.power
- サンプルサイズを誤るとエラーが起きる
- 便利なのはG power
統計学を学べる良書
私は大学院+独学で統計学を学び続けています
これまで参考になった統計学書は以下のものです













