研究を行っていると、結構な頻度で相関係数を算出することがあります
今回は、相関係数をpythonで算出する方法を解説していきたいと思います
また、以下の記事からpythonで統計学を順序立てて学ぶことができるようにまとめているので、参考にしてみてください
この記事で学べること
Pythonで相関係数を算出する方法
相関係数の基準
相関関係の可視化
データサイエンスの分野でも統計学は非常に重要になります
データサイエンスに興味がある方は、キカガクでデータサイエンスを学ぶのがおすすめです
キカガクはデータサイエンス・AI・機械学習に特化した動画学習プラットフォームです
相関係数とは
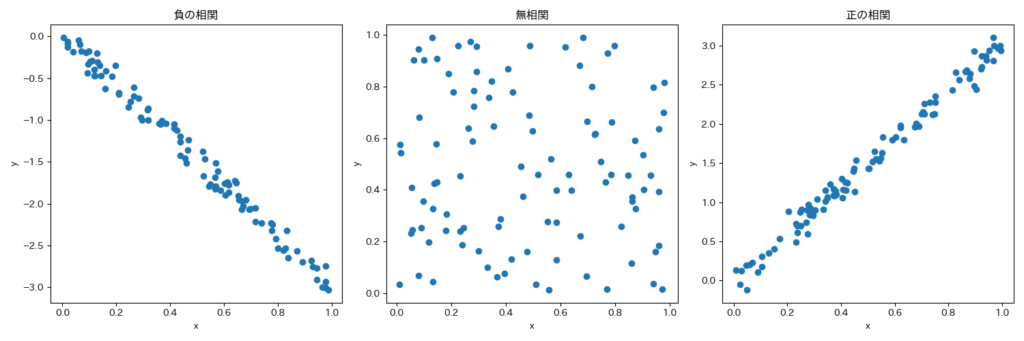
相関係数というのは、二つの値の間に関係性があるのか?ということを調べるために用います
相関係数を知る前に、相関関係について知っておく必要があります
例えば、Aという値が高く(低く)なれば、一方Bという値も高く(低く)なる、というのを相関関係と呼びます
この時、どのくらい関係しているのか?ということを示すのが、相関係数になります
相関係数の大小の基準
相関係数にはどのくらいの強さなのか?という一定の基準が設けられています
相関係数は-1〜1に収まるようになっており、基準は以下のようになっていますが、明確な基準はないとされています
これは、分野やデータの種類によって異なるためです

相関係数が0.7(-0.7)を超えれば相関は強い、
0.2(-0.2)以下であれば、ほとんど相関はないといって良いと思います
pythonで相関係数を算出する
pythonで相関係数を算出するには、numpyを使用して以下のようにコードを入力します
今回は国語と数学のテストの点数を例に挙げたいと思います
import numpy as np
import seaborn as sns
sns.set()
japanese = np.array([5, 73, 29, 63, 68, 28, 45, 78, 70, 93,82,88,98,68,78,12,32,18,19,22,34,14])
math = np.array([11, 82, 25, 61, 66, 27, 42, 88, 71, 84,82,95,58,87,68,22,38,15,23,43,15,22])
#相関係数の算出
correlation = np.corrcoef(japanese,math)
#グラフ化
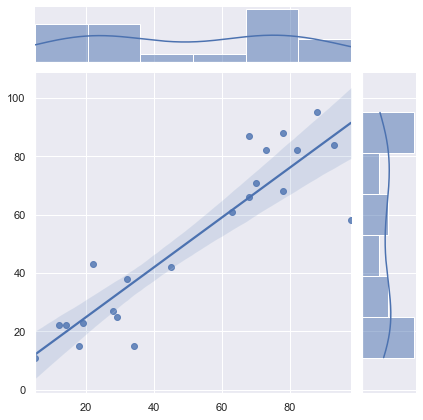
sns.jointplot(japanese, math, kind="reg")
print(correlation[0,1])
>>>出力結果
0.9049139268028888
各変数の相関の散布図を作成する
相関関係を確認したい変数が複数ある場合には、一度に散布図を作成して表示することも可能です
この時に使用するのは、seabornのpairplot()になります
irisのデータで実際に試していきたいと思います
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns; sns.set()
df = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv',index_col=0)
pg=sns.pairplot(df)
plt.show(pg)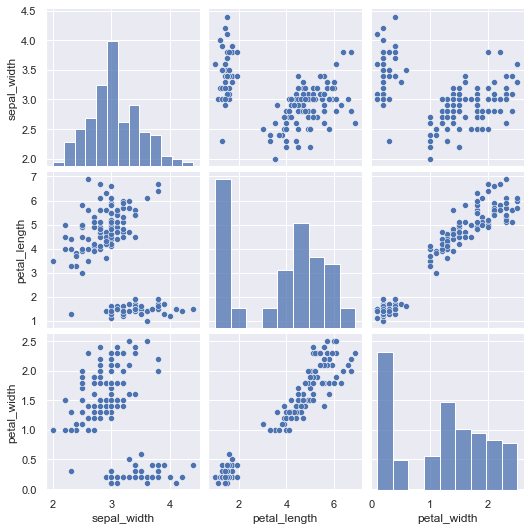
hueを追加することで、指定した列名のカテゴリごとに色分けをしたグラフが作成されます
今回はspeciesで色分けしたいと思います
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns; sns.set()
df = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv',index_col=0)
pg=sns.pairplot(df,hue='species')
plt.show(pg)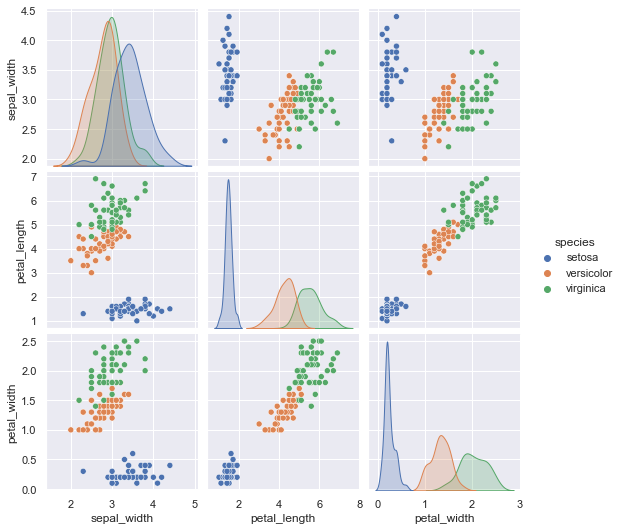
さらに回帰曲線を追加する場合には、kind=’reg’を入力します
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns; sns.set()
df = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv',index_col=0)
pg=sns.pairplot(df,hue='species', kind='reg')
plt.show(pg)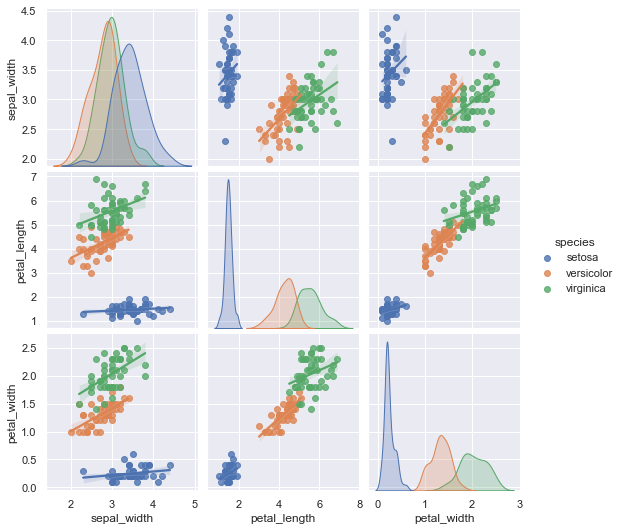
回帰曲線が少し見にくいので、以下のように変更します
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns; sns.set()
df = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/iris.csv',index_col=0)
pg=sns.pairplot(df,hue='species', kind='reg'
,plot_kws={'ci': None,'marker': '+','scatter_kws':
{'alpha': 0.4},'line_kws': {'linestyle': '--'}})
plt.show(pg)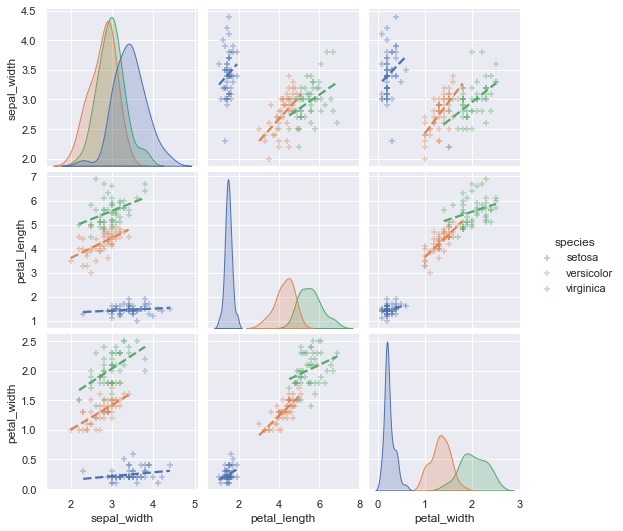
相関係数と因果関係は別物
相関関係があると、両者のデータ間に因果関係があるように捉えがちです
しかし、あくまでも相関係数は相関係数であって、因果関係とは別物です
よく例に上がるのが「身長と体重」の関係です
身長が高くなると体重も重くなる傾向にはありますが、
身長が高い人は必ずしも体重が重いわけではなく、身長が低い人は必ずしも体重が軽いわけではないですよね
また、体重が重くなると身長が高くなるわけではないですし、体重が軽くなると身長が低くなるわけでもないですよね
このように、どちらか一方がもう一方を決めるわけではないので、因果関係にあるとは言えません
仮に、身長が決まると体重も決定される、という世界があった場合には、これは因果関係と言えるでしょう
今回の例では、国語と数学の点数で相関係数を求めました
確かにこの両者には強い相関がありそうです
しかし、国語の点数が決まると数学の点数が決まるわけではないですよね?
なので、因果関係にあるとは言えません
相関係数と因果関係について学ぶには、次の書籍がおすすめです
相関係数と因果関係をごっちゃに考えてしまう方が多いので、この機会に一度学んでおくとデータサイエンティスト・データアナリティストとして、重宝される可能性が非常に高いです
相関係数と言われると、難しそうな数式を使っているイメージが多いかもしれませんが、こちらの書籍では、難しい数式を使わずに解説してくれています
pandasを使って相関係数を算出する
これまではnumpyを使って、相関係数を算出しましたが、pandasを使用して相関係数を算出することもできます
import pandas as pd
japanese =[5, 73, 29, 63, 68, 28, 45, 78, 70, 93,82,88,98,68,78,12,32,18,19,22,34,14]
math = [11, 82, 25, 61, 66, 27, 42, 88, 71, 84,82,95,58,87,68,22,38,15,23,43,15,22]
df_japanese=pd.DataFrame(japanese,columns=["japanese_score"])
df_math=pd.DataFrame(math,columns=["math_score"])
df=pd.concat([df_japanese,df_math],axis=1)
corr=df.corr()
print(corr)
>>>出力結果
japanese_score math_score
japanese_score 1.000000 0.904914
math_score 0.904914 1.000000numpyで算出した結果と同様の結果になりました
Scipyを使って相関係数を算出する
Pythonで相関係数を出すには、Scipyを使っても可能
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats
# データ生成
x = np.random.rand(100)
y = 2 * x + np.random.normal(0, 0.1, 100)
# ピアソンの相関係数
corrcoef_scipy_pearson, _ = scipy.stats.pearsonr(x, y)
# スピアマンの相関係数
corrcoef_scipy_spearman, _ = scipy.stats.spearmanr(x, y)
# 可視化
plt.scatter(x, y)
plt.title(f'SciPy Pearson: {corrcoef_scipy_pearson:.2f}, Spearman: {corrcoef_scipy_spearman:.2f}')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
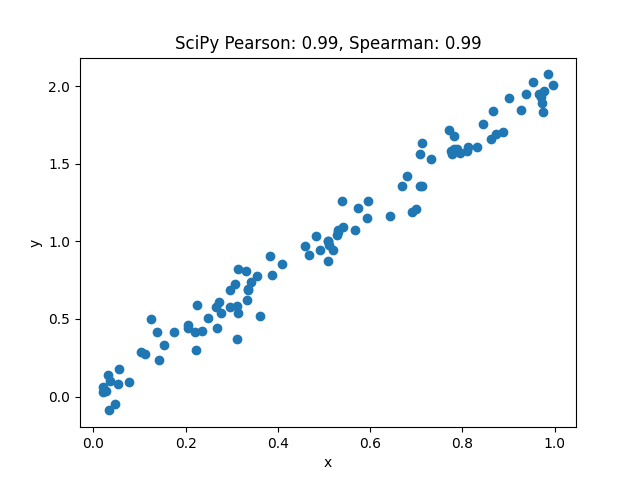
Pythonで相関係数の可視化
データ分析において、数値を出すだけでは意味がありません
相手に伝わりやすいよう、可視化をする必要があります
ここからは、Pythonで相関係数を可視化する方法を4つ紹介します
- 散布図
- バブルチャート
- グラフネットワーク
- ヒートマップ
散布図
import seaborn as sns; sns.set()
import matplotlib.pyplot as plt
import numpy as np
# 日本語フォントの指定(例: 'IPAexGothic')
plt.rcParams['font.family'] = 'IPAexGothic'
# データ生成
np.random.seed(0)
x = np.random.rand(100)
y = x * 2 + np.random.normal(0, 0.1, 100)
# 散布図
sns.scatterplot(x=x, y=y)
plt.title('散布図')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()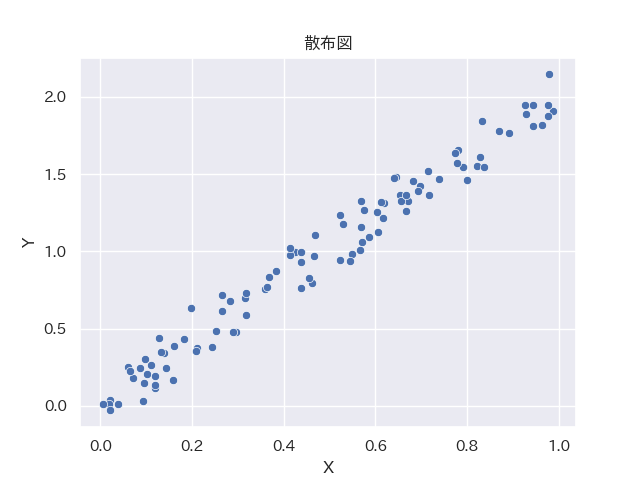
バブルチャート
import seaborn as sns; sns.set()
import matplotlib.pyplot as plt
import numpy as np
# 日本語フォントの指定(例: 'IPAexGothic')
plt.rcParams['font.family'] = 'IPAexGothic'
# データ生成
np.random.seed(0)
x = np.random.rand(100)
y = x * 2 + np.random.normal(0, 0.1, 100)
# サイズデータ生成(例としてxの値に応じたサイズ)
sizes = np.abs(x * 100)
# バブルチャート
sns.scatterplot(x=x, y=y, size=sizes, legend=False, sizes=(20, 200))
plt.title('バブルチャート')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()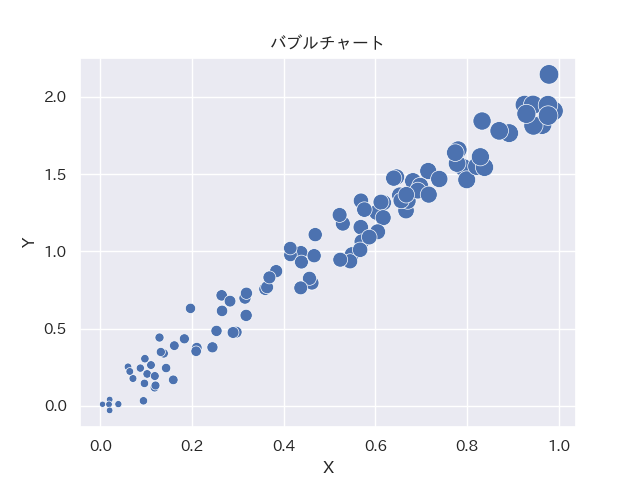
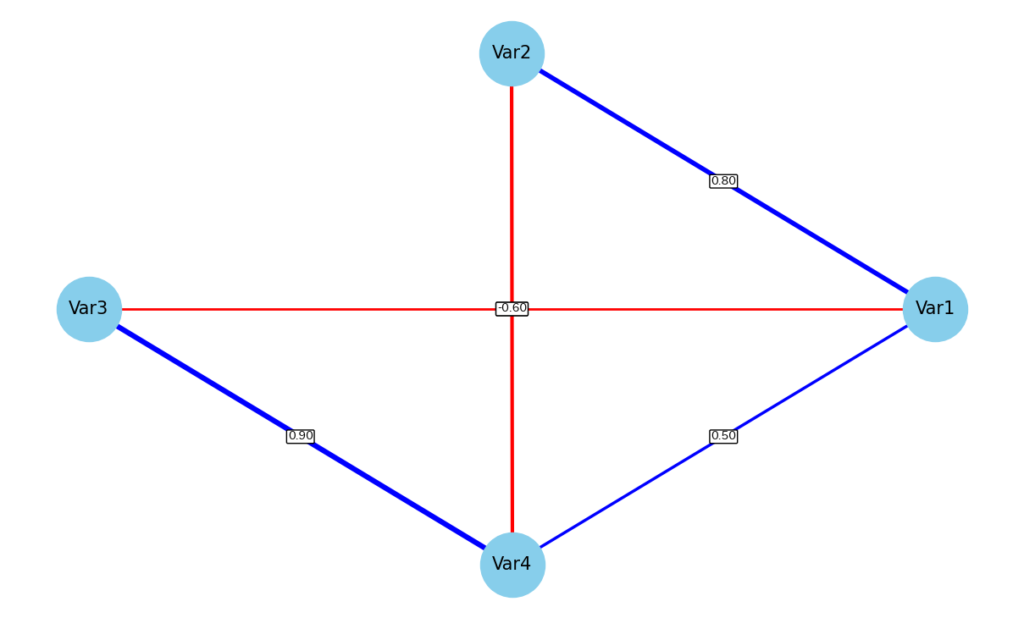
グラフネットワーク
グラフネットワークはseabornで作成することはできず、networkxというライブラリが必要です
import pandas as pd
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'IPAexGothic'
# 固定の相関行列を作成
corr_matrix = pd.DataFrame({
'Var1':  ,
'Var2': [0.8, 1, 0.3, -0.6],
'Var3': [-0.4, 0.3, 1, 0.9],
'Var4': [0.5, -0.6, 0.9, 1]
}, index=['Var1', 'Var2', 'Var3', 'Var4'])
# グラフネットワークの作成
G = nx.Graph()
# 相関行列を基にエッジを追加(相関係数の絶対値が特定の閾値を超える場合)
for i in range(len(corr_matrix.columns)):
for j in range(i+1, len(corr_matrix.columns)):
if np.abs(corr_matrix.iloc[i, j]) > 0.3:
G.add_edge(corr_matrix.columns[i], corr_matrix.columns[j], weight=corr_matrix.iloc[i, j])
# グラフネットワークの描画
pos = nx.circular_layout(G) # ノードの配置
edges, weights = zip(*nx.get_edge_attributes(G, 'weight').items())
edge_colors = ['blue' if weight > 0 else 'red' for weight in weights] # エッジの色
edge_widths = [5 * np.abs(weight) for weight in weights] # エッジの太さ
# edges=edgesは不要なので削除する
nx.draw(G, pos, with_labels=True, node_size=3000, node_color='skyblue',
edge_color=edge_colors, width=edge_widths, font_size=15)
# エッジラベルの描画(位置の調整を含む)
for edge in G.edges(data=True):
# エッジの中点を見つける
x0, y0 = pos[edge[0]]
x1, y1 = pos[edge
,
'Var2': [0.8, 1, 0.3, -0.6],
'Var3': [-0.4, 0.3, 1, 0.9],
'Var4': [0.5, -0.6, 0.9, 1]
}, index=['Var1', 'Var2', 'Var3', 'Var4'])
# グラフネットワークの作成
G = nx.Graph()
# 相関行列を基にエッジを追加(相関係数の絶対値が特定の閾値を超える場合)
for i in range(len(corr_matrix.columns)):
for j in range(i+1, len(corr_matrix.columns)):
if np.abs(corr_matrix.iloc[i, j]) > 0.3:
G.add_edge(corr_matrix.columns[i], corr_matrix.columns[j], weight=corr_matrix.iloc[i, j])
# グラフネットワークの描画
pos = nx.circular_layout(G) # ノードの配置
edges, weights = zip(*nx.get_edge_attributes(G, 'weight').items())
edge_colors = ['blue' if weight > 0 else 'red' for weight in weights] # エッジの色
edge_widths = [5 * np.abs(weight) for weight in weights] # エッジの太さ
# edges=edgesは不要なので削除する
nx.draw(G, pos, with_labels=True, node_size=3000, node_color='skyblue',
edge_color=edge_colors, width=edge_widths, font_size=15)
# エッジラベルの描画(位置の調整を含む)
for edge in G.edges(data=True):
# エッジの中点を見つける
x0, y0 = pos[edge[0]]
x1, y1 = pos[edge ]
x_mid = (x0 + x1) / 2
y_mid = (y0 + y1) / 2
# エッジの重み(相関係数)を取得
weight = edge
]
x_mid = (x0 + x1) / 2
y_mid = (y0 + y1) / 2
# エッジの重み(相関係数)を取得
weight = edge ['weight']
# エッジの重みに応じてラベルの位置を微調整
plt.text(x_mid, y_mid, f'{weight:.2f}',
horizontalalignment='center', verticalalignment='center',
bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.1'))
plt.title('変数間の相関係数を示したグラフネットワーク')
plt.axis('off') # 座標軸を非表示
plt.show()
['weight']
# エッジの重みに応じてラベルの位置を微調整
plt.text(x_mid, y_mid, f'{weight:.2f}',
horizontalalignment='center', verticalalignment='center',
bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.1'))
plt.title('変数間の相関係数を示したグラフネットワーク')
plt.axis('off') # 座標軸を非表示
plt.show()
ヒートマップ
最後に算出した相関係数をヒートマップで可視化していきます
ヒートマップの可視化にはseabornのheatmap()を使用します
import pandas as pd
import seaborn as sns
sns.set()
japanese =[5, 73, 29, 63, 68, 28, 45, 78, 70, 93,82,88,98,68,78,12,32,18,19,22,34,14]
math = [11, 82, 25, 61, 66, 27, 42, 88, 71, 84,82,95,58,87,68,22,38,15,23,43,15,22]
df_japanese=pd.DataFrame(japanese,columns=["japanese_score"])
df_math=pd.DataFrame(math,columns=["math_score"])
df=pd.concat([df_japanese,df_math],axis=1)
corr=df.corr()
print(corr)
sns.heatmap(corr,vmax=1,vmin=-1,center=0)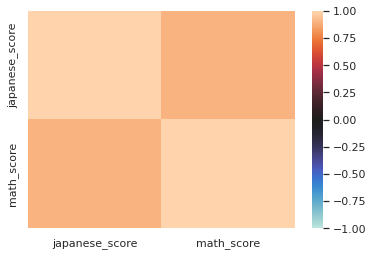
相関係数とp値を算出する
スピアマンの順位相関係数とピアソンの積率相関係数を使用すれば、相関係数とともにPythonでp値を算出することができます
スピアマンの順位相関係数・ピアソンの積率相関係数は、どちらもscipyを使用すると算出することができます
また、PandasとNumpyで算出している相関係数は、どちらもピアソンの積率相関係数です
スピアマンの順位相関係数
スピアマンの順位相関係数はscipyを使用すれば算出可能
from scipy import stats
math = [5, 73, 29, 63, 68, 28, 45, 78, 70, 93,82,88,98,68,78,12,32,18,19,22,34,14]
japanese = [11, 82, 25, 61, 66, 27, 42, 88, 71, 84,82,95,58,87,68,22,38,15,23,43,15,22]
correlation, pvalue = stats.spearmanr(math, japanese)
print(correlation,pvalue)
>>>出力結果
相関係数:0.8464801016852547 p値:6.854250491094454e-07ピアソンの積率相関係数
ピアソンの相関係数はscipy.pearsonrを使用します
from scipy import stats
math = [5, 73, 29, 63, 68, 28, 45, 78, 70, 93,82,88,98,68,78,12,32,18,19,22,34,14]
japanese = [11, 82, 25, 61, 66, 27, 42, 88, 71, 84,82,95,58,87,68,22,38,15,23,43,15,22]
correlation, pvalue = stats.pearsonr(math, japanese)
print(correlation,pvalue)
>>>出力結果
相関係数:0.9049139268028887 p値:7.328961270615418e-09今回のスピアマンの順位相関係数とピアソンの積率相関係数とpandas・numpyで算出した相関係数を比較すると、ピアソンの積率相関係数とpandas・numpyで算出した結果が同じになるため、pandasとnumpyはピアソンの積率相関係数を算出していると考えてOKです
スピアマンの順位相関係数とピアソンの積率相関係数の使い分けは以下のようになります

ノンパラ・パラメトリックについては以下の記事を参考にしてください

Pandasでピアソンの積率相関係数以外を算出する方法
Pandasで算出しているのは、ピアソンの積率相関係数ですが、Pandasのコードに手を加えると、「スピアマンの順位相関係数」と「ケンドールの順位相関係数」を算出できます
# スピアマンの順位相関係数
import pandas as pd
# データフレームの作成
data = {
'x':  ,
'y':
,
'y':  }
df = pd.DataFrame(data)
# スピアマンの順位相関係数を算出
spearman_corr = df.corr(method='spearman')
print(spearman_corr)
}
df = pd.DataFrame(data)
# スピアマンの順位相関係数を算出
spearman_corr = df.corr(method='spearman')
print(spearman_corr)
# ケンドールの順位相関係数
import pandas as pd
# データフレームの作成
data = {
'x':  ,
'y':
,
'y':  }
df = pd.DataFrame(data)
# ケンドールの順位相関係数を算出
kendall_corr = df.corr(method='kendall')
print(kendall_corr)
}
df = pd.DataFrame(data)
# ケンドールの順位相関係数を算出
kendall_corr = df.corr(method='kendall')
print(kendall_corr)
まとめ
- 相関係数は0.7を超えると強い相関、0.2以下はほぼ相関なし
- pandasとnumpyはピアソンの積率相関係数を算出している
- 相関係数と散布図を合わせてみる
- 相関関係と因果関係は別物
- pairplotはおしゃれ
pythonで統計学を学びたい方は、こちらを参考にしていただくと、一通り学ぶことができます

統計学だけではなく、データサイエンスに興味がある方は、キカガクでデータサイエンスを学ぶのがおすすめです
キカガクはデータサイエンス・AI・機械学習に特化した動画学習プラットフォームです
ちょっと気になるな…という方は、ぜひ説明会に参加してみてください
0からデータサイエンスを学び始める方に向けて、有料講座のプレゼントもあります
pythonで統計学を学ぶ上で必須書籍
pythonのスキルを高める方法
 pythonのスキルを高めるには、pythonを学べるプログラミングスクールに通うのが一つの方法です
pythonのスキルを高めるには、pythonを学べるプログラミングスクールに通うのが一つの方法です
以下の記事では、pythonが学べて、無料体験できるおすすめのプログラミングスクールを紹介しているので、ぜひ参考にしてみてください
これから先、pythonを使える社会人は重宝される時代が来るので、今のうちに学んでおくと、社会に出た時に有利に働きます





 ,
'Var2': [0.8, 1, 0.3, -0.6],
'Var3': [-0.4, 0.3, 1, 0.9],
'Var4': [0.5, -0.6, 0.9, 1]
}, index=['Var1', 'Var2', 'Var3', 'Var4'])
# グラフネットワークの作成
G = nx.Graph()
# 相関行列を基にエッジを追加(相関係数の絶対値が特定の閾値を超える場合)
for i in range(len(corr_matrix.columns)):
for j in range(i+1, len(corr_matrix.columns)):
if np.abs(corr_matrix.iloc[i, j]) > 0.3:
G.add_edge(corr_matrix.columns[i], corr_matrix.columns[j], weight=corr_matrix.iloc[i, j])
# グラフネットワークの描画
pos = nx.circular_layout(G) # ノードの配置
edges, weights = zip(*nx.get_edge_attributes(G, 'weight').items())
edge_colors = ['blue' if weight > 0 else 'red' for weight in weights] # エッジの色
edge_widths = [5 * np.abs(weight) for weight in weights] # エッジの太さ
# edges=edgesは不要なので削除する
nx.draw(G, pos, with_labels=True, node_size=3000, node_color='skyblue',
edge_color=edge_colors, width=edge_widths, font_size=15)
# エッジラベルの描画(位置の調整を含む)
for edge in G.edges(data=True):
# エッジの中点を見つける
x0, y0 = pos[edge[0]]
x1, y1 = pos[edge
,
'Var2': [0.8, 1, 0.3, -0.6],
'Var3': [-0.4, 0.3, 1, 0.9],
'Var4': [0.5, -0.6, 0.9, 1]
}, index=['Var1', 'Var2', 'Var3', 'Var4'])
# グラフネットワークの作成
G = nx.Graph()
# 相関行列を基にエッジを追加(相関係数の絶対値が特定の閾値を超える場合)
for i in range(len(corr_matrix.columns)):
for j in range(i+1, len(corr_matrix.columns)):
if np.abs(corr_matrix.iloc[i, j]) > 0.3:
G.add_edge(corr_matrix.columns[i], corr_matrix.columns[j], weight=corr_matrix.iloc[i, j])
# グラフネットワークの描画
pos = nx.circular_layout(G) # ノードの配置
edges, weights = zip(*nx.get_edge_attributes(G, 'weight').items())
edge_colors = ['blue' if weight > 0 else 'red' for weight in weights] # エッジの色
edge_widths = [5 * np.abs(weight) for weight in weights] # エッジの太さ
# edges=edgesは不要なので削除する
nx.draw(G, pos, with_labels=True, node_size=3000, node_color='skyblue',
edge_color=edge_colors, width=edge_widths, font_size=15)
# エッジラベルの描画(位置の調整を含む)
for edge in G.edges(data=True):
# エッジの中点を見つける
x0, y0 = pos[edge[0]]
x1, y1 = pos[edge ['weight']
# エッジの重みに応じてラベルの位置を微調整
plt.text(x_mid, y_mid, f'{weight:.2f}',
horizontalalignment='center', verticalalignment='center',
bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.1'))
plt.title('変数間の相関係数を示したグラフネットワーク')
plt.axis('off') # 座標軸を非表示
plt.show()
['weight']
# エッジの重みに応じてラベルの位置を微調整
plt.text(x_mid, y_mid, f'{weight:.2f}',
horizontalalignment='center', verticalalignment='center',
bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.1'))
plt.title('変数間の相関係数を示したグラフネットワーク')
plt.axis('off') # 座標軸を非表示
plt.show()












