マーケティングに活用可能！統計分析をPythonで実行する方法

マーケティングは商品が売れる仕組みを作り上げていくことに重きが置かれていますが、仕組みを作るのと同じくらい大切なことがあります

それが、なぜ売れたのか？なぜ売れなかったのか？という点を分析することです

なぜ売れたのか？売れなかったのか？については、統計分析を活用することで、要因が明確になり、マーケティングに活用することができます

この記事では、初心者にも優しいPythonというプログラミング言語を使って、マーケティングに活用可能な統計分析をPythonで実行していきたいと思います

統計分析以外の分析手法を知りたい方は、以下の記事でよく使われる分析手法を解説しているので、参考にしてください

>>>Pythonでマーケティングに活用できるデータ分析手法を公開【サンプルコードあり】

マーケティングで統計分析はどれを使う？

統計分析と一言で言っても、分析手法はいくつもありますし、統計の中にも種類があります

ここではまず統計の種類について理解を深め、どの統計を使うべきかを考えていきたいと思います

推測統計

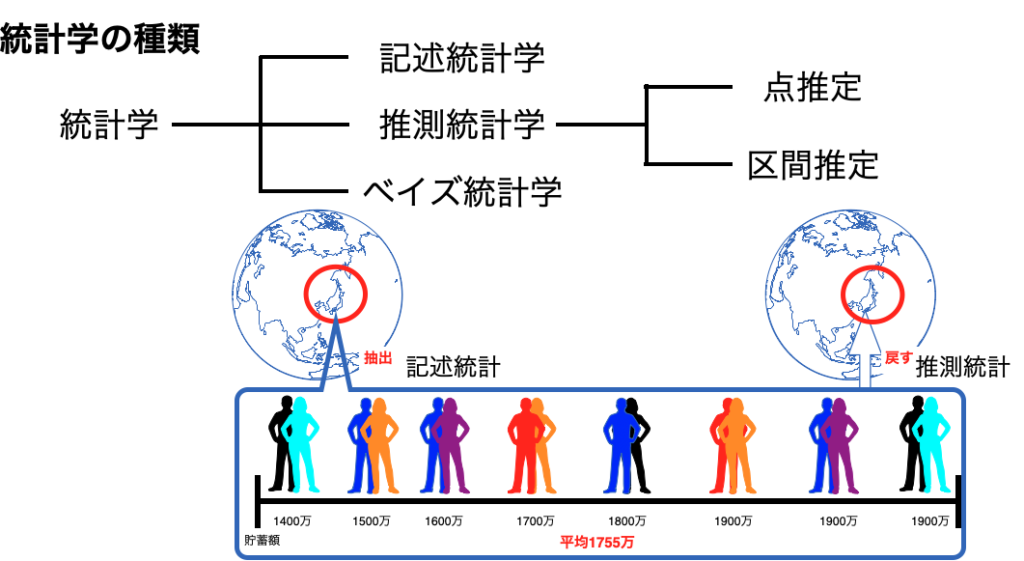
推測統計学とは、サンプルから得られたデータをもとに、母集団の特性についての統計的な推測を行います

母集団とは、全ての対象物の集合のことを指し、サンプルはその一部のデータの集合を意味しています

推測統計学は、サンプルから得られたデータをもとに、母集団全体の平均値や分散、相関関係などの統計的特性を推定します

具体的には、点推定や区間推定、仮説検定、回帰分析などの手法が用いられます

推測統計学を使うことによって、少ないサンプルから得られた情報を活用し、より正確に全体の推測を行うことができます

例えば、ある製品の評価について、全ての消費者の意見を調査することは困難ですが、一部消費者からのサンプルデータをもとに、製品全体についての評価を推測することが可能です

記述統計

記述統計学とは、データの集計、整理、要約、可視化などを通じて、データの特性を理解していきます

具体的には、平均、中央値、標準偏差、最大値・最小値、四分位数などの統計量を計算し、ヒストグラム、箱ひげ図、散布図などのグラフなどを作成します

記述統計学は、データの性質や傾向を理解するために用いられます

また、複数の製品の販売実績を比較するために、箱ひげ図を作成することで、中央値や分散、外れ値の有無などを比較することもできます

記述統計学によって、データの傾向や特性を理解することで、適切な分析手法を選択することができます

また、データの傾向を把握することで、ビジネス上の課題や機会を発見することもできます

推測統計と記述統計について、理解を深めたい方は、こちらの記事を参考にしてください

【pythonで統計学】推測統計学と記述統計学について統計学は大きく分けて3種類あります記述統計学推測統計学ベイズ統計学 t検定などの「統計的仮説検定」を用...

例えば、ある製品の販売実績について、月ごとの売上高を集計してヒストグラムを作成することで、売上高の分布やピークの時期を把握することができます

ベイズ統計

ベイズ統計は、ベイズの定理を用いた統計学の一種で、データと事前情報を組み合わせることで、事後確率分布を推定する統計手法です

従来の頻度主義的な統計学に対し、ベイズ統計は、データが与えられた場合のパラメータの不確実性を考慮することができます

ベイズ統計では、パラメータを確率変数として扱い、事前分布と呼ばれる確率分布を設定します

そして、データが観測された後、ベイズの定理により、事後分布を推定します

この事後分布は、データと事前分布に基づいて更新されたパラメータの確率分布であり、パラメータの推定値や不確実性を評価することができます

ベイズ統計は、小規模なデータやパラメータが少ない場合に有効であり、分析結果の解釈が容易であるという特徴があります

また、事前知識や事前分布を反映することができるため、過学習を回避することができるというメリットもあります

マーケティングと統計分析の関係性

マーケティングにおいて発生する膨大なデータを集め、整理、解釈して、市場のトレンドや顧客の行動パターンなどを分析し、ビジネス上の意思決定をサポートすることが出来るのが、統計分析です

例えば、広告やキャンペーン、プロモーションなどの効果を分析するために、広告のクリック数やコンバージョン率、消費者の属性や行動データなどを収集し、統計的な手法を用いて解析します

また、マーケティング調査や顧客満足度調査などで得られたデータを分析することもあります

マーケティングと統計分析を行うことで、マーケティング戦略の改善や、新しい製品やサービスの開発、販売促進の方法の最適化などが可能になります

マーケティングで活用できる統計分析手法5選

ここからはマーケティングで活用できる統計分析手法を5つ紹介していきます

実際にPythonで実装できるように、サンプルコードも掲載していきますので、Pythonでの実装にチャレンジしてみてください

回帰分析

回帰分析とは、ある変数（説明変数）と別の変数（目的変数）との関係を分析するための統計手法の一つで、教師あり学習の代表例です

具体的には、説明変数が目的変数にどのような影響を与えるかを分析し、それを数式化することで、ある説明変数の値から目的変数の値を予測することができます

回帰分析には、

線形回帰分析
非線形回帰分析
多重回帰分析
ロジスティック回帰分析

などがあります

それぞれの分析手法は、分析するデータの性質や目的に合わせて選択されます

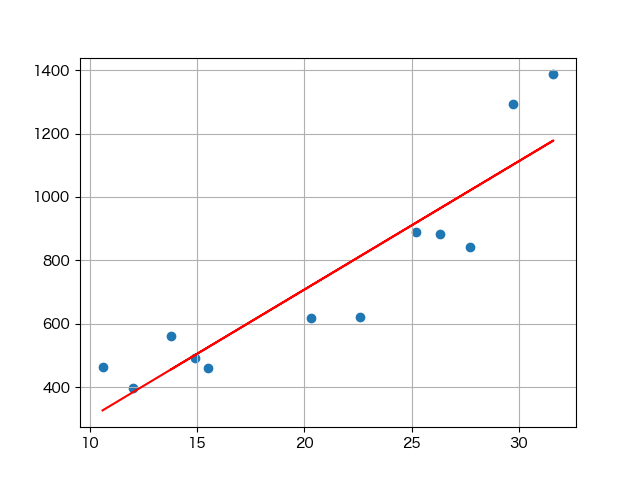
例えば、マーケティングの分野では、ある商品の売り上げがどのような要因によって変動するのかを分析するために回帰分析が用いられます

回帰分析をPythonで実装する際には、以下のように実装していきます

(コードで入力していたのですが、文字化けっぽくなってしまったので、スクショでごめんなさい)

SVM（サポートベクターマシン）

サポートベクターマシン（Support Vector Machine、SVM）は、機械学習の分野において、分類や回帰に用いられる教師あり学習アルゴリズムの一種です

SVMは、データの集合を分類する境界線（決定境界）を見つけることで、新しいデータがどちらのクラスに属するかを予測します

SVMの特徴は、決定境界と最も近いデータ点（サポートベクター）の距離を最大化するように決定境界を定めることにあります

これにより、決定境界が最も一般化されたものになるため、過学習を避け、未知のデータに対する予測精度を高めることができます

SVMは、線形カーネルや非線形カーネルなどのカーネル関数を用いることで、非線形なデータの分類も可能です

SVMは、データが疎である場合や、データ数が多い場合でも高速に処理することができます

そのため、画像認識やテキスト分類などの分野で広く用いられています

SVMは、データの前処理やハイパーパラメータの調整が必要であり、実装が難しい場合もあります

しかし、高い予測精度を得られることが多く、機械学習の分野において重要なアルゴリズムの一つとなっています

バスケット分析

バスケット分析（Basket Analysis）は、売り上げデータなどの取引データを分析する手法の一つです

この手法では、同時に購入される傾向がある商品の組み合わせを発見することで、販売促進やクロスセルの提案などに活用されます

バスケット分析は、主に以下の手順で行われます。

集めたい売り上げデータを収集する
売り上げデータを取引ごとに分割し、商品単位で集計する
全取引データから商品の出現回数、同時に出現する商品の組み合わせの出現回数を集計する
出現回数が高い商品の組み合わせを抽出し、顧客に商品を紹介する

例えば、コンビニでのバスケット分析を考えてみます

ある日、コンビニでの販売データを取得し、そのデータを商品ごとに集計したところ、以下のような結果が得られました

ビール 100本
ポテトチップス 50袋
ピーナッツ 40袋
コーラ 80本
スナック菓子 30袋

このデータを用いてバスケット分析を行うと、ビールとポテトチップス、ビールとピーナッツ、コーラとスナック菓子のように、同時に購入される商品の組み合わせを発見することができます

こうした組み合わせを知ることで、コーナーのレイアウトの改善や商品の販促、セット販売などに活用することができます

バスケット分析は、小売業やECサイトなど、さまざまな分野で活用されています

クラスタリング分析

機械学習で使われるクラスタリングは、データの類似度によって、データをグループ分けする方法になります

例えば、企業の広告メールで考えてみます

若者向けの新商品ができた場合、過去に商品を購入してくれた顧客100名に対して、全く同じ内容のメールを送信すれば、労力は少なくて済みますが、新商品が売れるかどうかわかりません

若者向けの既存商品を購入してくれたことがある顧客のみにメールを送れば、費用を抑えることが出来ますし、購入確率も上がります

過去に購入した商品は、年代別や類似した商品の購入など、さまざまなパターンがありますが、このようなパターンを見つけ出し、グループ分けを行なっていくのが、クラスタリングになります

クラスタリングは、マーケティングやレコメンドエンジンのアルゴリズムなどに活用されています

クラスタリングを実装してみたい方は、以下の記事にサンプルコードを掲載しているので、参考にしてください

Pythonで機械学習のクラスタリングを実装する【サンプルコードあり】この記事では、Pythonで機械学習のクラスタリングを実装していきます。クラスタリングは機械学習の中でも教師なし学習に分類される、機械学習です。PythonではK-meansを使ったクラスタリングを簡単に実装することができるので、一緒に実装していきましょう。...

主成分分析

主成分分析（Principal Component Analysis, PCA）とは、多次元データの変数間に存在する相関を利用して、データを新しい軸（主成分）上に射影することで、データの情報を圧縮し、可視化や分析の効率化を図る手法です

主成分分析は、以下のような手順で行われます

元データの標準化：各変数の平均を0、標準偏差を1にすることで、変数の尺度差を解消します。
共分散行列の算出：変数間の相関係数から共分散行列を求めます。
固有値・固有ベクトルの算出：共分散行列の固有値と固有ベクトルを算出します。
主成分の選択：固有値の大きい順に主成分を選択します。
主成分スコアの算出：元データを選択した主成分に射影することで、主成分スコアを算出します

主成分分析によって、元データの変数間の相関関係を把握し、そのうち重要な情報を取り出すことができ、統計解析や機械学習、画像処理など、幅広い分野で応用されています

例えば、マーケティング分野では、購買データの分析に主成分分析を適用し、消費者の購買行動に影響を与える要因を把握することができます

また、医療分野では、複数のバイオマーカーを用いた疾患診断に主成分分析を適用し、診断精度を向上させることができます

主成分分析をPythonで実装するには、以下のようなコードになります

今回は、scikit-learnに用意されているワインデータを使って次元削減を行なっていきます

from matplotlib import pyplot as plt from 
sklearn import datasets 
import numpy as np 
from sklearn.decomposition import PCA

 # datasetの読み込み
 wine_data = datasets.load_wine()
 df=wine_data.data
 Y=wine_data.target  print(df.shape)
  #主成分分析 
pca=PCA(n_components = 2, whiten = False)
 pca.fit(df)  
# データを主成分に変換する
 features = pca.transform(df) 
print(features.shape)  
# 主成分をプロットする
 #色かえ 
for label in np.unique(Y):
     if label == 0:         
         c = "red"     
    elif label == 1: 
         c="blue"  
    elif label == 2:
         c="green"    
    else: 
         pass     
plt.scatter(features[Y == label,0], 
            features[Y == label,1],                
            c=c)
 plt.title('principal component') 
plt.xlabel('Z1')
 plt.ylabel('Z2') 
plt.savefig('PCA_sample1')
 plt.show()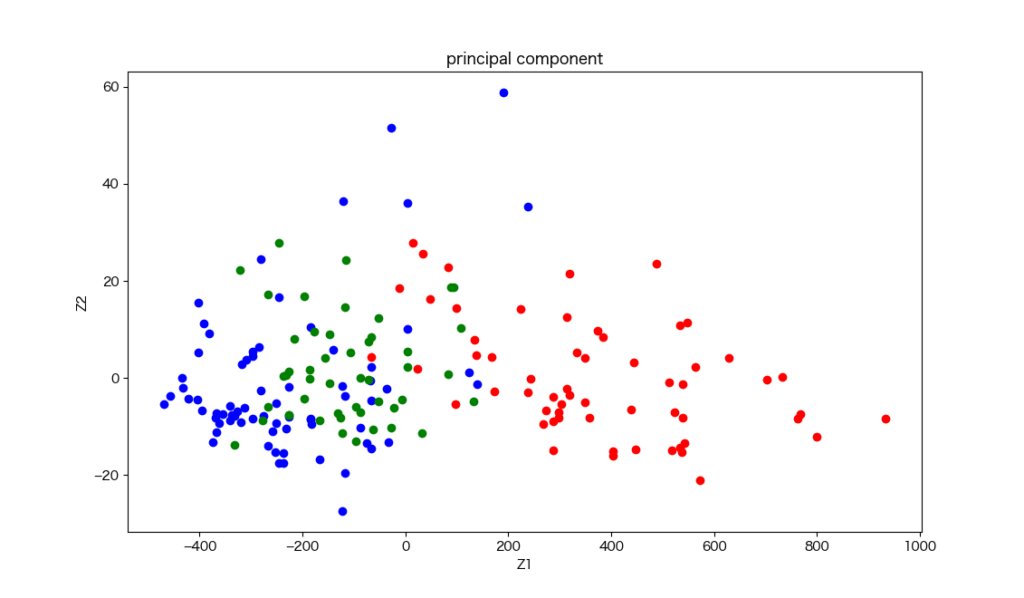

主成分分析を実行後にクラスタリングを実装するサンプルコード

from matplotlib import pyplot as plt
from sklearn import datasets
import numpy as np
from sklearn.decomposition import PCA
import pandas as pd
from sklearn.cluster import KMeans  

#データ読み込み
wine_data = datasets.load_wine()
df=wine_data.data
Y=wine_data.target
#主成分分析の実装
pca=PCA(n_components = 2,whiten=False)
pca.fit(df)
feature=pca.transform(df)
#実装した主成分分析をデータフレームに変換し,PC1とPC2というカラム名をつける
existing_df_2d = pd.DataFrame(feature)
existing_df_2d.columns = ['PC1','PC2']
#クラスタリングの実装
kmeans = KMeans(n_clusters=5)
clusters = kmeans.fit(existing_df_2d)
existing_df_2d['cluster'] = pd.Series(clusters.labels_, index=existing_df_2d.index)
#クラスタリングの結果を可視化
existing_df_2d.plot(
        kind='scatter',
        x='PC2',y='PC1',
        c=existing_df_2d.cluster.astype(np.float),
        s=existing_df_2d['PC2']*100,
        figsize=(16,8))
plt.show()

機械学習について

機械学習には、教師なし学習・教師あり学習・強化学習があります

教師あり学習とは、事前に与えられた情報をもとに、学習を行なっていく手法です

教師なし学習とは、事前に情報を与えられることなく、手元のデータをグループ分けしていくことになります

また、強化学習というのは、ある特定の行動(や動作)を取った際に報酬(評価)が与えられ、最も多く報酬を得られるように試行錯誤しながら、学習していく手法です

教師あり学習は、分類や回帰に利用されるケースが多く、教師なし学習は、グループ分けや情報の要約などに利用されます

強化学習の例として、アルファ碁というものがあります

>>>「囲碁AI」の最強時代到来、プロ棋士の存在価値は薄れてしまうのか？

教師あり学習

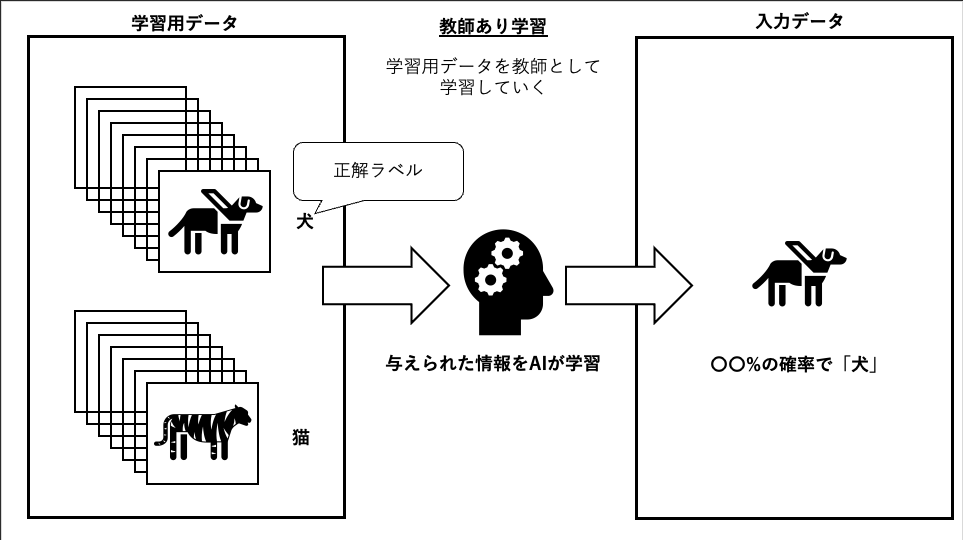
教師あり学習とは、プログラムに正解となる学習データを与え、学習させる手法です

学習データを教師として、与えられたデータで学習を進めていき、未知なるデータが入力されたときに、学習データに基づき、出力を予測するのが教師あり学習になります

すでに与えられているデータに「犬」や「猫」と名称をつけることを「ラベル付け」と呼びます

教師あり学習は、分類と回帰で使用されることが多く、画像認識や文章分類、音声認識などに活用されています

分類：入力データを複数に分けることが目的
回帰：入力データから連続的な出力値を予測するのが目的

Pythonで機械学習の教師あり学習を行う場合には、次のようなライブラリがあります

scikit-learn：分類、回帰、クラスタリング、次元削減などの機械学習アルゴリズムを提供する優れたライブラリ
TensorFlow：深層学習 (Deep Learning) アルゴリズムを提供する人気のライブラリ
PyTorch：TensorFlowに代わる人気のDeep Learningフレームワーク

教師なし学習

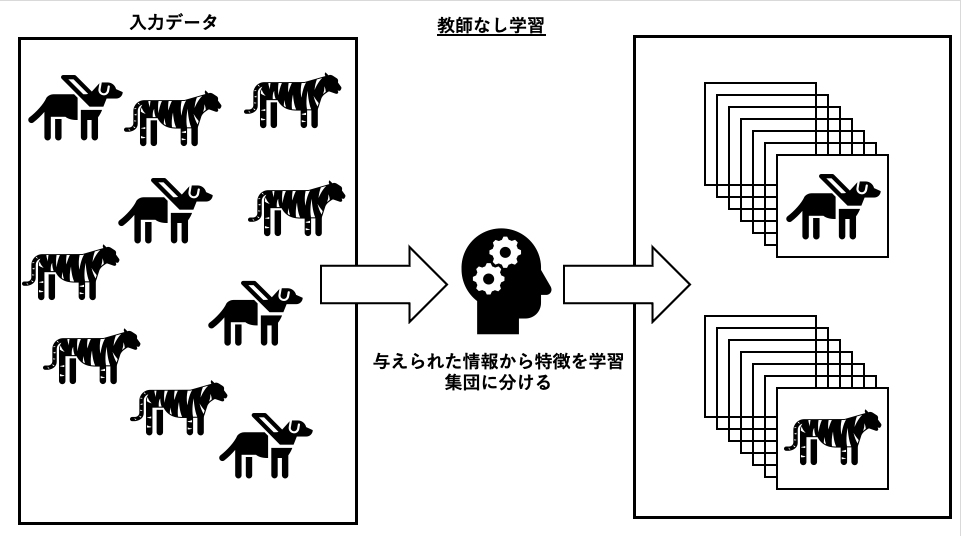
教師なし学習は、入力データにラベル付けがされておらず、与えられたデータに隠されている特徴や構造を学習します

学習した後に、いくつかに集団にグループ分けを行うのが、教師なし学習になります

このとき分けられたグループの特徴や構造がどういったものなのかは、データ解析者の判断が必要になります

教師なし学習はクラスタリングと次元削減などに活用されており、データ探索やデータ可視化、異常検知などで活用されています

クラスタリング：入力データをグループに分けることを目的とします
次元削減：高次元データを低次元データに圧縮するのが目的です

Pythonで機械学習の教師なし学習を行う場合には、次のようなライブラリがあります

scikit-learn：分類、回帰、クラスタリング、次元削減などの機械学習アルゴリズムを提供する優れたライブラリです。
SciPy：数値計算、信号処理、統計などのライブラリの一つです。教師なし学習にも使われます。
NumPy：数値計算を行うためのライブラリです。

クラスタリングの実装は、次の記事でサンプルコード付きで解説しているので、参考にしてください

強化学習

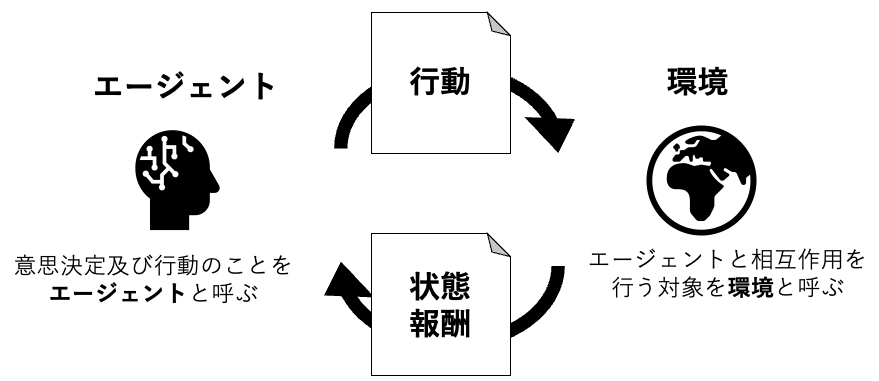
強化学習とは、エージェントが環境とやり取りをすることで、最適な行動を学習する機械学習です

強化学習では、エージェントが環境から受け取る報酬を最大化するように、行動を選択することで、学習を行なっていきます

強化学習には、様々なアルゴリズムがあります

例えば、「Q学習」は、行動を選択するためのQ値を求めることで、最適な行動を学習したり、「SARSA」は、状態と行動を同時に求めるアルゴリズムです

Pythonで強化学習を行うためのライブラリとして、次のようなものがあります

OpenAI Gym：OpenAI Gymを使うことで、様々なタスクを設定して、エージェントを学習させることができます
stable-baselines：OpenAI Gymを使った強化学習のためのライブラリです
table-baselinesでは、Q学習やSARSA、強化学習に基づく強化学習アルゴリズムを実装しており、簡単に強化学習を実装することができます。
TensorFlow-Agents：Googleが提供する、TensorFlowを使った強化学習のためのライブラリ
TensorFlow-Agentsでは、深層学習を使った強化学習アルゴリズムを実装しており、高度な強化学習タスクを実現することができます。

機械学習とAI・ディープラーニングの関係性

機械学習とAI・ディープラーニングの関係性は図にするとわかりやすいです

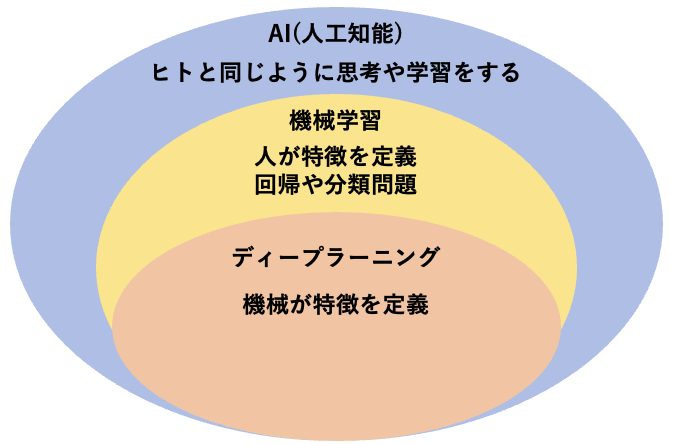
AIの中には、機械学習やディープラーニングが含まれており、機械学習にはディープラーニングが含まれています

そのため、AIを開発するためには、機械学習・ディープラーニングの理解が必須になります

機械学習やディープラーニングを理解するには、データミックスの活用がおすすめです

無料で個別相談を予約する

データミックスの口コミを調べる

※無料オンライン相談や個別相談などさまざまなイベントが開催中

マーケティングに統計分析を用いるメリット3つ

ここからはマーケティングに統計分析を用いるメリットについて、3つ解説をしていきます

「マーケティング×統計分析」ができる人材は少数のため、学んでおくことで希少性の高い人材になれます

今回紹介するメリットは、次の3つです

課題の特定と改善
予測の精度向上
効果測定の客観化

課題の特定と改善

マーケティングにおいては、統計分析を活用することで、

データに基づいた意思決定ができる
ターゲット層を正確に把握できる
製品やサービスの改善ができる
マーケティング戦略の改善ができる

など、課題の特定と改善を行うことができます

統計分析を用いることで、販売促進活動の成果を客観的に評価し、どのような課題があるかを特定することもできます

予測の精度向上

マーケティングにおいては、将来の需要や売上高を予測することも重要で、統計解析を用いることで、

顧客行動の予測が可能になる
リソースの最適化ができる
競合他社の動向を予測できる

といったメリットがあります

統計分析を用いることで、製品の購入傾向やキャンペーンへの反応、サイトの訪問数など将来的な顧客行動を予測することができます

また、競合他社の広告出稿量やプロモーションの展開、新製品の発売予定などを分析することで、将来的な市場動向を予測することができます

効果測定の客観化

マーケティングにおいては、マーケティングの効果を測定することは非常に重要です

しかし、その効果を測定するためには、何をもって効果とするか、という基準を設定する必要があります

統計分析を用いることで、基準を客観的に設定し、販売促進活動の効果を客観的に評価することができます

これにより、販売促進活動の改善や、施策の見直しができるようになります

例えば、売上を予測する線形回帰モデルを作成し、そのモデルを用いてキャンペーンの効果測定を行ってみます

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 乱数のシードを指定
np.random.seed(123)

# 同じ値を設定
campaign_budget = np.full(1000, 10000)
ad_spend = np.full(1000, 500)
email_spend = np.full(1000, 100)
organic_spend = np.full(1000, 50)
sales = np.random.randint(1000, 100000, 1000)

# 辞書型のデータを作成
data = {'campaign_budget': campaign_budget,
        'ad_spend': ad_spend,
        'email_spend': email_spend,
        'organic_spend': organic_spend,
        'sales': sales}


# DataFrameを作成
df = pd.DataFrame(data)
print(df)

# データを表示
print(df.head())
X = df.drop('sales', axis=1)
y = df['sales']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

model = LinearRegression()
model.fit(X_train, y_train)

y_pred = model.predict(X_test)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
r2 = r2_score(y_test, y_pred)
print("RMSE: ", rmse)
print("R^2: ", r2)

campaign_budget = 15000
ad_spend = 1000
email_spend =200
organic_spend = 500

campaign_data = [[campaign_budget, ad_spend, email_spend, organic_spend]]
campaign_sales = model.predict(campaign_data)
print("Expected sales: ", campaign_sales[0])

ここで予測された売り上げと実際の売上を比較して、そのキャンペーンの効果測定を行うことができます

また、複数のキャンペーンを比較し、どのキャンペーンが最も効果的であるかを客観的に測定することもできます